All Contents
Overview

Consider a kindergartener who dazzles her family with enthusiastic displays of her counting prowess. Or a second grader who eagerly spots quadrilaterals on a walk around the neighborhood. Think about a mischievous third grader who uses his developing knowledge of fractions to trick unsuspecting peers with the question, "How many numbers are between one and two?" Our youngest learners deserve teachers who will ignite their mathematical curiosity and confidence, because building competence in math can change their lives.

Math matters. For elementary-age students, higher math scores tend to translate to higher earnings as adults.1 In fact, math scores predict future earnings better than reading scores. Early math skills are also a strong predictor of success in other subjects, like reading and science, and even grade retention from kindergarten through eighth grade.2 To reap the benefits associated with high math achievement, students need opportunities to develop a strong foundation in the elementary years. Mathematics knowledge is highly cumulative in nature, meaning that students who struggle to learn foundational math concepts are likely to continue to struggle well into middle and high school.3

Unfortunately, many elementary students in the United States do not receive adequate math instruction. Nearly a quarter of fourth graders, over 850,000 children in the U.S.4—roughly the entire population of San Francisco—lack basic math knowledge and skills, such as locating numbers on a number line or subtracting multidigit whole numbers.5

Improving math achievement for students starts with ensuring that their teachers have the knowledge and skills they need to teach effectively. There is a persistent misconception that anyone with a high school diploma has the requisite math knowledge to teach elementary math. In reality, teaching elementary math requires both a conceptual understanding of foundational mathematics and pedagogical knowledge of how to teach the concepts.6

Teachers need to know how to do more than just follow the steps in math to get the right answer. They need to know why those steps work. It's like the difference between a basketball player and a coach. The player can follow directions and specialize in their role, but the coach needs to understand the bigger picture—the why behind every move. In other words, teachers need to deeply understand the math they want students to learn and must have the specialized knowledge of how to teach it, including recognizing and correcting student misconceptions.

Elementary teachers themselves report that they do not feel ready to provide strong math instruction. Many elementary teachers do not feel adequately well prepared to teach many areas of math.7 In fact, one in four elementary teachers reports feeling anxious doing math.8 Teachers suffering from math anxiety have a negative impact on their students' math outcomes.9 Providing aspiring teachers with strong preparation offers an antidote to math anxiety by helping them become the confident and competent math instructors students need.

Teacher prep experience infographic

Teacher preparation programs are well situated to play a key role in solving the math problem. To do so, they must dedicate sufficient time to develop aspiring teachers' math content and pedagogical knowledge. In NCTQ's latest examination of over 1,100 elementary teacher prep programs, we find most programs do not provide teacher candidates with enough time to develop math content knowledge. This is especially true of graduate prep programs. Prep programs failing to commit the necessary instructional time for math must reevaluate their priorities or they will continue to deny the nation's students effective math instruction and its many associated benefits.

Findings

Most undergraduate programs devote enough overall time to mathematics, but do not allocate that time adequately across key content topics and math pedagogy.

Setting program requirements is a difficult task, a balancing act of competing priorities vying for limited time. Program leaders have to consider state and university policy, as well as the full range of knowledge elementary teachers need. Even when focusing just on mathematics, programs must overcome two distinct challenges.

  • First, prep programs must carve out a sufficient number of credit hours to address the full range of content and pedagogical knowledge elementary teachers need to provide effective math instruction.

  • Once the necessary courses are in place, programs must then ensure that adequate time is allocated to cover each of the four key content topics: numbers & operations, algebraic thinking, geometry & measurement, and data analysis & probability; as well as mathematics-specific pedagogy.

This analysis provides insight into where programs succeed and struggle on these two fronts.

NCTQ's instructional hour targets under the Elementary Mathematics standard provide a benchmark for how much coursework programs should provide and how programs should distribute that course time. These targets are widely agreed upon by practitioners in the field. NCTQ derived these targets from feedback obtained during an open comment period in 2021 and recommendations from NCTQ's Expert Advisory Panel, a group of mathematicians, math educators, and representatives from teacher preparation programs.10

Recommended instructional hour targets for each essential math topic, NCTQ revised Elementary Mathematics standard

Content

PEDAGOGY

Numbers & operations

Algebraic thinking

Geometry & measurement

Data analysis & probability

Mathematics pedagogy

Total

45
Instructional hours

20
Instructional hours

25
Instructional hours

15
Instructional hours

45
Instructional hours

150
Instructional hours

One full 3-credit course

Just under half of a 3-credit course

Just over half of a 3-credit course

One-third of a 3-credit course

One full 3-credit course

10 credits

A note about time

NCTQ bases instructional hours on course credits. One semester credit equates to 15 hours of instruction. Therefore, a typical three-credit course is 45 instructional hours. NCTQ adjusts the credit hours for institutions with academic calendars not based on semester credit hours (e.g., quarter credit hour counts are adjusted so that each credit equals 15 instructional hours).

Three credit course infographic
Most undergraduate programs meet or approach the overall target of 150 hours of instructional time on math

The good news is nearly two-thirds of undergraduate programs rise to the first challenge by either setting aside enough instructional time or falling just short. Nearly two in five (39%) programs fully meet the overall target of at least 150 hours of specialized mathematics coursework. Another 23% of programs fall short by no more than 15 hours, the equivalent of a single course credit. This indicates that many programs already have adequate time set aside to prepare teachers well in math. The remaining programs vary widely in the amount of math instructional time they provide, including four undergraduate programs that require no teacher audience math coursework at all.

Overall time undergraduate programs dedicate to elementary math coursework

Adequate
(>150 hours)

39%

Nearly adequate
(135-149 hours)

23%

Not adequate
(<135 hours)

38%
Many undergraduate programs do not use their instructional time to adequately cover the four key content topics

Most programs dedicate enough (or nearly enough) time to math, yet do not focus enough of the time on the four key content topic areas. As the chart below shows, the average undergraduate program exceeds the time needed for math pedagogy, yet falls short of the instructional hours needed to develop teacher candidates' foundational understanding of math content. In particular, programs are not dedicating enough time to numbers & operations and algebraic thinking.

On average, undergraduate programs fall short of the target instructional hours for math content and exceed the target for math pedagogy.
0
15
30
45
60
75
90
105
Mathematics Content
85
85 hours

The average number of instructional hours in mathematics content provided by undergraduate programs.

105
105 hours

The minimum number of instructional hours to adequately address elementary mathematics content.

Mathematics Pedagogy
51
51 hours

The average number of instructional hours in mathematics pedagogy provided by undergraduate programs.

45
45 hours

The minimum number of instructional hours to adequately address elementary mathematics pedagogy.

Number of instructional hours

Program average
Recommended minimum Info icon
The minimum number of instructional hours required to address this topic area. See the full Methodology for more information.

(n=838 programs) On average, programs in the sample allocate sufficient time to math pedagogy, exceeding the recommended target of 45 instructional hours. However, the average program provides about 80% (85 hours) of the recommended time of 105 hours to essential mathematics content. This figure does not include 28 undergraduate programs for which full analysis could not be completed.

0
15
30
45
60
75
90
105
120
135
150
Numbers & Operations + Algebraic Thinking (combined) Info icon
The number of hours estimated for Numbers & Operations and Algebraic Thinking are treated together because course descriptions often combine the two topics. This may occur because student standards (such as the Common Core State Mathematics Standards) combine Operations and Algebraic Thinking through the mid-elementary grades, with Algebra becoming more of a separate topic in later grades.
49
49 hours

The average number of instructional hours in Numbers & Operations + Algebraic Thinking (combined) provided by undergraduate programs.

65
65 hours

The minimum number of instructional hours to adequately address Numbers & Operations + Algebraic Thinking (combined).

Geometry & Measurement
24
24 hours

The average number of instructional hours in Geometry & Measurement provided by undergraduate programs.

25
25 hours

The minimum number of instructional hours to adequately address Geometry & Measurement.

Data Analysis & Probability
13
13 hours

The average number of instructional hours in Data Analysis & Probability provided by undergraduate programs.

15
15 hours

The minimum number of instructional hours to adequately address Data Analysis & Probability.

Mathematics Pedagogy
49
49 hours

The average number of instructional hours in mathematics pedagogy provided by undergraduate programs.

45
45 hours

The minimum number of instructional hours to adequately address elementary mathematics pedagogy.

Total
134
134 hours

The average number of instructional hours in mathematics content and pedagogy provided by undergraduate programs.

150
150 hours

The minimum number of instructional hours to adequately address elementary mathematics content and pedagogy.

Number of instructional hours

Program average
Recommended minimum Info icon
The minimum number of instructional hours required to address this topic area. See the full Methodology for more information.
Undergraduate program grades highlight that too many programs fail to adequately distribute instructional time dedicated to mathematics.

The Elementary Math standard uses letter grades to identify programs that dedicate enough overall time to math and distribute that time to ensure that candidates learn the core content across all topics that they are likely to teach. To earn an A grade, a program must address at least 90% of the recommended target for each of the five topic areas.

Despite often dedicating enough course time to math, only one in every six undergraduate programs spends enough time on essential math content. While 62% of the total sample require at least three math courses and have the potential to earn an A by adequately distributing instructional time across the key content topics, only 16% of programs ultimately meet the second challenge and achieve this goal.

Undergraduate program grades on the Elementary Mathematics standard show little change from 2022 to 2025

Grades are based on program coverage of the key content topics of elementary mathematics instruction, including numbers & operations, algebraic thinking, geometry & measurement, and data analysis & probability, as well as mathematics pedagogy. The grades for 28 additional programs in the sample could not be determined and were excluded. The grades for 2025 do not sum to 100% due to rounding.

These findings reveal that little has changed over the last three years. As we saw in 2022, even among programs that have allocated sufficient time to math, too many fail to provide the necessary breadth and depth of content. More often than not, undergraduate programs shortchange the time dedicated to the four content topics and instead spend too much time on pedagogy. Notably, this pattern appears to be more prevalent in some states than others.

Regent University

Regent University: Increasing instructional time for math

Regent University is a private, Christian university based in Virginia Beach, Virginia. The university offers several licensure-track teacher preparation programs, the most popular of which is the Elementary Education program. Regent's program earned an A+ in our current Teacher Prep Review: Solving for Math Success analysis, up from a D grade in 2022. The improved grade is based on two key changes program leaders made: (1) replacing a general statistics course with a probability and statistics course specifically for teachers and (2) adding a numbers & operations course for teachers as an additional program requirement.

Learn more

The average graduate program dedicates 14 hours of instructional time—less than one course credit—to foundational math content knowledge.

Undergraduate and graduate programs are preparing candidates for the same job. Candidates entering a graduate program hold undergraduate degrees in fields outside of education that would not have required the specialized coursework elementary teachers require. Because of this, there is no excuse for graduate programs, which are offering initial certifications in teaching, to provide candidates with any less preparation in mathematics than their undergraduate counterparts. Yet that is precisely what NCTQ's analysis reveals.

Info icon
What about alternative certification programs?

Past Teacher Prep Review reports presented the results of nontraditional programs alongside those of traditional programs. However, due to the opaque nature of many prominent alternative certification programs, NCTQ is not able to complete a parallel analysis under this standard.

It is important to note that there is no one alternative certification program model. These programs range from models that closely resemble two-year graduate programs to those that immediately place candidates as teachers of record with little or no preparation. NCTQ does not support any teacher preparation model in which candidates immediately serve as teachers of record while still completing foundational coursework. Aside from states requiring candidates to pass licensing tests before entering the classroom, which effectively makes it a condition of program admissions, there is no reason to expect that one-year alternative programs provide any better preparation than traditional graduate programs, which consistently lack time on essential math content.

In late 2025, NCTQ will publish a guide defining the range of alternative certification programs to support the field in drawing distinctions between models.

Very few graduate programs meet or approach the target of 150 hours of instructional time on math

In 2022, NCTQ found graduate elementary programs were dedicating an average of just 14 hours of instruction to mathematics content knowledge, which is less than one-third of a typical three-credit course. The story remains unchanged in 2025. We continue to find that graduate programs spend less than a single course credit to address concepts like algebraic thinking, geometry, and probability. In fact, just 5% of graduate programs meet or approach the target of 150 hours of mathematics instruction.

The limited instructional time graduate programs dedicate to math is predominantly focused on pedagogy, offering little check that candidates know the content before expecting them to learn how to teach it. As graduate and alternative programs continue to grow in prominence, it is not surprising that student math scores remain stagnant.

On average, graduate programs fall far below the target instructional hours for math content and for math pedagogy.
0
15
30
45
60
75
90
105
Mathematics Content
14
14 hours

The average number of instructional hours in mathematics content provided by graduate programs.

105
105 hours

The minimum number of instructional hours to adequately address elementary mathematics content.

Mathematics Pedagogy
38
38 hours

The average number of instructional hours in mathematics pedagogy provided by graduate programs.

45
45 hours

The minimum number of instructional hours to adequately address elementary mathematics pedagogy.

Number of instructional hours

Program average
Recommended minimum Info icon
The minimum number of instructional hours required to address this topic area. See the full Methodology for more information.

(n=318 programs) On average, graduate programs do not allocate sufficient time to math content or pedagogy. While graduate programs collectively approach the recommended time of 45 hours of mathematics pedagogy, the average program provides only 13% (14 hours) of the recommended time of 105 hours to essential mathematics content. This figure does not include the four graduate programs for which full analysis could not be completed.

0
15
30
45
60
75
90
105
120
135
150
Numbers & Operations + Algebraic Thinking (combined) Info icon
The number of hours estimated for Numbers & Operations and Algebraic Thinking are treated together because course descriptions often combine the two topics. This may occur because student standards (such as the Common Core State Mathematics Standards) combine Operations and Algebraic Thinking through the mid-elementary grades, with Algebra becoming more of a separate topic in later grades.
9
9 hours

The average number of instructional hours in Numbers & Operations + Algebraic Thinking (combined) provided by graduate programs.

65
65 hours

The minimum number of instructional hours to adequately address Numbers & Operations + Algebraic Thinking (combined).

Geometry & Measurement
3
3 hours

The average number of instructional hours in Geometry & Measurement provided by graduate programs.

25
25 hours

The minimum number of instructional hours to adequately address Geometry & Measurement.

Data Analysis & Probability
2
2 hours

The average number of instructional hours in Data Analysis & Probability provided by graduate programs.

15
15 hours

The minimum number of instructional hours to adequately address Data Analysis & Probability.

Mathematics Pedagogy
38
38 hours

The average number of instructional hours in mathematics pedagogy provided by graduate programs.

45
45 hours

The minimum number of instructional hours to adequately address elementary mathematics pedagogy.

Total
52
52 hours

The average number of instructional hours in mathematics content and pedagogy provided by graduate programs.

150
150 hours

The minimum number of instructional hours to adequately address elementary mathematics content and pedagogy.

Number of instructional hours

Program average
Recommended minimum Info icon
The minimum number of instructional hours required to address this topic area. See the full Methodology for more information.

Aspiring elementary teachers need math coursework designed for them, rather than math courses intended for any college student as part of their general education requirements. The Mathematical Education of Teachers II (MET II) report states, "It bears emphasizing that familiar mathematics courses such as college algebra, mathematical modeling, liberal arts mathematics, and even calculus or higher level courses are not an appropriate substitute for the study of mathematics for elementary teachers, although they might make reasonable additions" (emphasis in original).11 Yet the vast majority of graduate programs continue to rely on the general audience math coursework candidates completed as undergraduates as validation of adequate content knowledge. Because of this reliance on potentially irrelevant coursework, this analysis finds no improvement in graduate programs' preparation since 2022.

Graduate program grades highlight that nearly all graduate programs fail to provide candidates adequate time to build math content knowledge and pedagogy

The Elementary Mathematics standard applies the same expectations to both undergraduate and graduate programs. Graduate programs fall far short of providing the math instruction candidates need: More than 8 in 10 graduate programs earn an F.

Graduate program grades on the Elementary Mathematics standard show little change from 2022 to 2025

Grades are based on program coverage of the key content topics of elementary mathematics instruction, including numbers & operations, algebraic thinking, geometry & measurement, data analysis & probability, as well as mathematics pedagogy. The grades for four additional programs in the sample could not be determined and were excluded. The grades for 2025 do not sum to 100% due to rounding.

Important to note is that the Elementary Mathematics methodology gives instructional hour credit to programs that validate content knowledge at admissions through the use of content-knowledge tests as a proxy for course requirements. Using an adequate test at admissions offers both an opportunity to verify that candidates have relevant knowledge and to identify candidates who may need additional math support.12 However, among the 318 graduate programs we reviewed, just 6% use such a test, with most that do earning a B.

It's particularly useful when looking at graduate programs to consider how they compare to their undergraduate counterparts on the same campus. Despite the fact that both undergraduate and graduate programs at the same institution are preparing aspiring teachers for the same career, they are rarely aligned in how they define adequate preparation. In fact, on average, undergraduate programs dedicate nearly six times as many hours to teaching math content as graduate programs on the same campus.

Comparing mathematics instructional hours between undergraduate and graduate programs on the same campus

  • Undergraduate

    133 hours of 150 hours
    Total hours

    Undergraduate programs in total spend 81 hours more on mathematics instruction than graduate programs

    Graduate

    52 hours of 150 hours
  • 83 hours of 105 hours
    Mathematics content

    Undergraduate programs spend 68 hours more on mathematics pedagogy than graduate programs

    15 hours of 105 hours
  • 50 hours of 45 hours
    Mathematics pedagogy

    Undergraduate programs spend 13 hours more on mathematics pedagogy than graduate programs

    Undergraduate programs exceed the recommended hours on mathematics pedagogy by 5 hours

    37 hours of 45 hours

(n=233 institutions) The average graduate program dedicates narrowly more than a single course to elementary math content and pedagogy. In contrast, undergraduate programs on the same campus average three courses.

University of Montana: Aligning coursework for all elementary teacher candidates

Among the many degree and course offerings at the Phyllis J. Washington College of Education at the University of Montana are both an undergraduate and graduate pathway to initial elementary education licensure. Bucking the national trend, both programs earn an A+, just as they did in 2022. (Both programs also earned an A+ under the Teacher Prep Review: Reading Foundations standard in 2023.)

Learn more

Top Performing Programs

These 83 exemplary programs earn an A+ because they meet 100% of the target instructional hours under each of the five topics.

Texas
Stephen F. Austin State University
A+ Undergraduate
Improved 2022 grade: B
Washington
University of Washington - Tacoma
A+ Undergraduate
Ohio
Bowling Green State University
A+ Undergraduate
Improved 2022 grade: B
Louisiana
Louisiana Tech University
A+ Undergraduate
California
California State University - Long Beach
A+ Undergraduate
Montana
University of Montana
A+ Graduate
Georgia
Dalton State College
A+ Undergraduate
Virginia
Regent University
A+ Undergraduate
Improved 2022 grade: D
Show more See all program scores

Findings by State

When looking at undergraduate prep programs' course requirements across the country, clear differences emerge between states. Undergraduate programs in 14 states, including Maryland, Oklahoma, Oregon, and Utah average at least seven credits (105 instructional hours) of coursework focused on mathematics content knowledge. In contrast, programs in Florida, Missouri, New Jersey, New York, and Vermont average half that amount of time.

Findings by State: Average instructional hours allocated for math preparation in undergraduate elementary programs
Unintended consequences: How state policy can create barriers in teacher preparation

Undergraduate elementary programs in virtually all states are just like any other major. Once general education requirements are satisfied, prep program leaders have control over the remaining time, which normally translates to two-plus years of coursework (60-75 credit hours). This is not the case in all states though. For example, New York state policy mandates elementary teacher candidates must complete a content major outside of education, leaving elementary programs a fraction of the time afforded to programs in most other states to cover important math coursework. The effect of this policy can be seen in the graph above. Looking across content and pedagogical coursework, undergraduate programs in New York collectively dedicate the second least amount of instructional time to mathematics.13

While New York's policy remains in place, neighboring New Jersey has codified a positive policy change that will take effect in September 2025.14 Elementary programs will have control over 30 more credits (a full year of coursework), and the state has mandated that programs dedicate six to nine of those credits to specialized math courses. While these policy changes alone will not ensure that programs implement coursework adhering to research-supported approaches, the collective change reflects a clear understanding of the credit limitations programs have faced and the need to designate course time to high-priority areas, including mathematics.

Recommendations

It is incumbent upon both teacher preparation programs and the states that serve as their regulators to identify viable approaches to ensure all teacher candidates are ready for their first day in the classroom. To that end, we offer eight ways teacher preparation program leaders and state policymakers can make the necessary progress:

Actions for Teacher Prep Programs

1

Dedicate at least 150 instructional hours—10 credits—to elementary mathematics and ensure required coursework provides the necessary instructional time to address the content knowledge and pedagogy teachers need.

Absent information from strong diagnostic testing at the point of admissions, most candidates will need both content and pedagogy courses. Three content courses and one course in pedagogy is common among top performing programs, though many programs successfully integrate content and pedagogy within courses. Specifically, elementary teachers need a strong conceptual understanding of numbers & operations, algebraic thinking, geometry & measurement, and data analysis & probability; in addition to math pedagogy. This knowledge is specialized and should be aimed at a teacher audience, not the broader campus population. Providing this amount of time is achievable. Learn from examples of top-performing programs that are getting math instruction right.

2

Graduate programs unable to dedicate additional instructional hours to mathematics should require content-knowledge tests as a condition of admission to diagnose where candidates need additional support and coursework rather than rejecting applicants.

Employing a content-knowledge test as part of admission does not mean that programs need to turn down candidates who fail. Programs can admit candidates conditionally with additional course requirements to address knowledge gaps. Even with such a provision in place, graduate programs still need to increase the overall time dedicated to mathematics coursework specific to teacher candidates.

3

Build partnerships with nearby districts to create feedback loops specific to elementary mathematics instruction.

Given that it will be districts that have to make up for lack of content knowledge among new teachers, programs and districts should come together to review course materials and content expectations for teacher candidates to determine if the program is meeting districts' needs. Consider using focus groups, surveys, and data on student growth and teacher evaluation to understand which key topic areas recent teacher candidates were well-prepared to teach and which they were not, and use that information to drive changes in the prep program's math coursework.

4

Ensure student teaching placements occur with cooperating teachers who are effective mathematics instructors.

Student teachers who are paired with a more effective cooperating teacher are more effective in their first year of teaching. Programs should also consider how well-versed their program supervisors are in math content, to ensure that they can provide candidates with accurate and content-specific feedback during classroom observations. NCTQ's Clinical Practice Action Guide offers a host of resources for programs to improve their clinical practice policies and procedures.

Actions for State Policymakers

1

Use sound policy to support teacher prep programs and hold them accountable for producing teacher candidates who are prepared to teach math.

NCTQ's June 2025 State of the States report on the mathematics policy landscape will provide state policymakers with feedback on standards for elementary teacher prep related to math content and coursework, as well as on the state's requirements around program approval (including whether the process reviews syllabi from math courses, whether math experts are involved, and whether the state uses math licensure test pass rate data in program approval).

2

Revise policies that prevent prep programs from dedicating additional instructional hours for mathematics instruction.

Review state regulations and policies related to teacher preparation to ensure that teacher preparation programs are able to provide adequate instructional time for math content and pedagogy (see examples of New York and New Jersey described above).

3

Require that all elementary teacher prep programs dedicate adequate course time to mathematics.

As seen in the data, graduate programs typically require too little specialized mathematics coursework for teachers, with content knowledge-focused coursework most often excluded from requirements.

4

Require all elementary teacher candidates to pass a strong mathematics licensing test.

The quality of content-knowledge tests varies greatly across the country. In many instances, these tests do not evaluate mathematics independent of other subject areas. In the absence of minimum coursework requirements for all elementary teacher candidates, it is necessary to evaluate knowledge through a high-quality assessment.

How We Scored

The 2025 Elementary Mathematics sample includes 1,188 programs, with at least one program from every state and the District of Columbia. These undergraduate and graduate programs are housed in 942 institutions of higher education (IHEs) that offer elementary teacher preparation leading to initial licensure. The sample is generally inclusive of all public institutions that actively produce elementary teachers and all private institutions with an annual production of at least 10 elementary teachers (based on program enrollment counts from Title II).

Evaluation relies on two sources of data to produce a preliminary score for each program to review before the score is finalized:

  • Course syllabi

  • Course descriptions

To determine the validity of using course descriptions in lieu of syllabi, a pilot test evaluated 200 courses for which both course descriptions and syllabi were available to arrive at two independent assessments for how much time was dedicated to each of the five topics. The two forms of analysis produced similar results on average, within a range of 10 percentage points for each of the five topics. Further, the distribution of program grades under the two approaches was highly correlated, with no notable bias towards either approach. For more details from this pilot study, go here.

Methodology in brief

A team of analysts use course catalogs to determine the required coursework for each elementary program in the sample. Analysts then read course titles and descriptions to pinpoint all courses that are inclusive of mathematics. Teacher audience mathematics courses, inclusive of those that focus on both content and pedagogy are flagged for analysis. General audience mathematics courses (College Algebra, for example) are excluded from analysis.

A separate team of expert mathematics analysts evaluate syllabi and course descriptions using a detailed scoring protocol. Each course is analyzed for its coverage of five topics:

  • Numbers and Operations

  • Algebraic Thinking

  • Geometry and Measurement

  • Data Analysis and Probability

  • Mathematics Pedagogy

Two additional topic categories of "Other Content Topics" and "Other Pedagogy Topics" are also included in the coding process so that non-relevant material (science pedagogy, for example) can be accounted for while coding the totality of each course.

Course descriptions for every course are independently evaluated by two analysts. Twenty percent of syllabi are randomly selected to be scored by a second analyst. In both cases, disagreements are adjudicated by a third analyst.

Course coding

When coding a Course Description

When coding a Syllabus

Reference Count

Count of the total number of references to each identifiable topic (e.g., Numbers and Operations)

Unit Type

Identify the type of calendar (daily, weekly, etc.) used in the syllabus.

Unit Count

Identify the total number of units (days, weeks, etc.) that are defined in the course schedule.

Reference Count

For each unit, count of the total number of references to each identifiable topic.
 

Within the course description or details presented in the syllabus...

Within each unit specified in the syllabus...

1. Numbers and Operations

Count of the number of references to Numbers and Operations including any subtopics within that domain.

2. Algebraic Thinking

Count of the number of references to Algebraic Thinking, including any subtopics with that domain.

3. Geometry and Measurement

Count of the number of references to Geometry and Measurement including any subtopics with that domain.

4. Data Analysis and Probability

Count of the number of references to Data Analysis and Probability, including any subtopics with that domain.

5. Mathematics Pedagogy

Count of the number of references to mathematics instructional approaches.

6. Other Content Topics

Count of the number of references that address mathematics content topics outside any of the four content areas (e.g., references to trigonometry or calculus).

7. Other Pedagogy Topics

Count of the number of references that address general pedagogy or subject-specific pedagogy for subjects other than mathematics.

After coding all courses, the percentage of each course dedicated to each topic is calculated. The resulting percentages are multiplied by the total instructional hours for the course (1 semester credit hour is equal to 15 instructional hours). The instructional hour counts are summed across all courses within a program and those values are measured against the scoring rubric.

NCTQ produced preliminary findings based on course descriptions and shared those findings with prep programs. Then we gave programs a month to provide additional course material to improve the accuracy of the findings. NCTQ provided multiple reminders during this timeframe to ensure that prep programs had ample opportunities to review their findings and provide further information.

Info icon
Learn more about the development and scoring of the Elementary Mathematics standard.
See the full Technical Manual for Elementary Mathematics (2022) for details on the development of the standard, the sample of programs, scoring protocols, coding reliability between data sources, and supporting research.

A program's instructional hours under each topic are measured against individual targets. Instructional hours are counted up to the target, but not beyond, which means a program cannot make up for a lack of hours under one topic with excess in another. However, there is one exception.

While Numbers and Operations and Algebraic Thinking are separately coded and reported, for the purposes of scoring, the two topics are considered together. The result is that excess hours under either of those individual topic targets can be applied to the combined target.

Instructional hour targets

Numbers & Operations

Algebraic Thinking

Geometry & Measurement

Data Analysis & Probability

Math Pedagogy

Total

45 hours

20 hours

25 hours

15 hours

45 hours

150 hours

65 hours

Programs that require a passing score on a content knowledge licensing test as a condition of admissions into the preparation program automatically receive credit for 80% of the instructional hour targets for the four content topics (not Math Pedagogy), which is then added to the instructional hours these programs require through content coursework for the purpose of scoring this standard. The 80% credit is only given under this measure in instances where the content knowledge licensing test has an independent cut score for mathematics.

Grade rubric

Grade

Total Percentage of Instructional Hours Target

A+

At least 150 instructional hours across the five topics and 100% of the recommended target hours under each of the five topics.

A

At least 135 instructional hours across the five topics and at least 90% of the recommended target hours under each of the five topics

B

At least 120 instructional hours (80%) across the five topics

C

At least 105 instructional hours (70%) across the five topics

D

At least 90 instructional hours (60%) across the five topics

F

Fewer than 90 instructional hours (less than 60%) across the five topics

Note: In cases where a syllabus is not available and the course description does not provide enough detail to be coded, the course is designated as "couldn't be determined" (CBD). When that designation is applied to any course within a program, the program's grade is listed as "CBD."

Does mathematical content knowledge matter for elementary teachers?

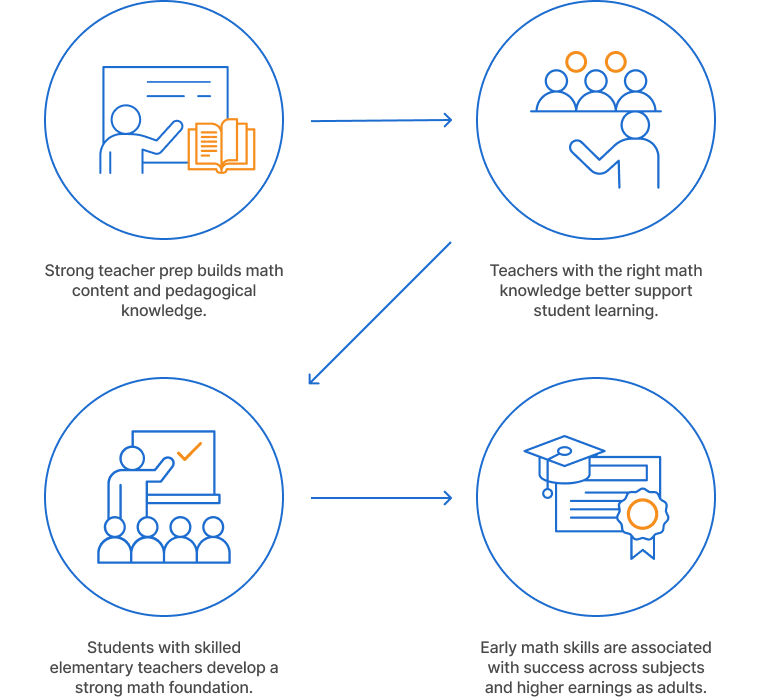
In general, elementary students achieve more in math when taught by teachers with greater mathematics content knowledge.15

Unfortunately, completing a bachelor's degree or a teacher preparation program does not guarantee that teachers know the math they'll be expected to teach. One study found that many elementary teacher candidates had misconceptions about statistics and probability as they were about to enter student teaching (the culminating experience of most teacher preparation programs).16 A national survey found that few elementary teachers felt very well-prepared to teach specific elementary mathematics topics, and the proportion who felt very well-prepared declined between 2012 and 2018.17 This sense of inadequate preparation has persisted for decades; in 2002, surveys of elementary teachers in Michigan and Ohio18 indicate that they did not feel well prepared to teach the specific mathematics topics at the elementary level or slightly beyond.

Most research finds that teacher candidates' mathematics coursework seems to yield benefits for their students. Several studies demonstrated that teachers deliver stronger lessons on topics that they learned in their teacher preparation programs.19 One study of teacher preparation programs (both traditional and alternative) in New York City found that math courses correlated with increased student achievement in math during the second year of teaching,20 and another study found that not only the number of content courses but also the types of courses matters for building candidates' knowledge,21 although one study found no correlation between teachers' math education credits and student achievement in math.22

How much coursework do elementary teacher candidates need?

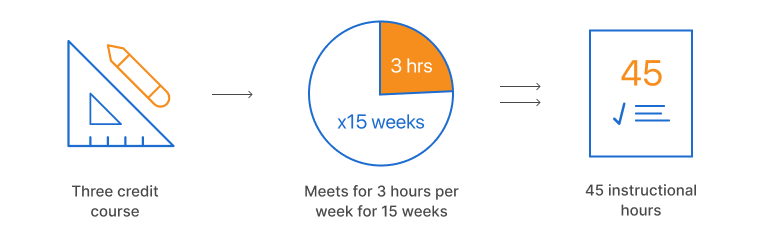
Prospective elementary teachers need mathematics courses which are designed specifically for teachers and which impart a deep understanding of elementary and middle school mathematics concepts.23 The Conference Board of the Mathematical Sciences (CBMS)24 recommends that aspiring elementary teachers take 12 semester-credit hours in "elementary mathematics content" covering numbers and operations, algebra, measurement and data, and geometry, while the National Council of Teachers of Mathematics (NCTM)25 recommends taking at least three college-level mathematics courses in the content essential to elementary grades, in addition to instruction on pedagogy.26 The Mathematical Education of Teachers II (MET II) study draws from the Common Core State Standards to recommend that elementary teachers be prepared in the domains of counting and cardinality, operations and algebraic thinking, numbers and operations, measurement and data, and geometry, as well as connections to mathematics topics typically addressed in the middle grades.27

Some research casts doubt on the extent to which current teacher preparation programs adequately meet the mathematics needs of aspiring elementary teachers. Several surveys of over 400 institutions, taken 6 years apart, found that most were not meeting the recommendation that elementary candidates take at least 12 semester credit-hours of mathematics content.28 Another study found that mathematics content courses were inconsistent in whether they engaged teacher candidates in the Common Core Standards for Mathematical Practice.29

What types of math courses should elementary teacher candidates take?

The preponderance of available research indicates that the mathematics content coursework needed by elementary teachers is neither pure mathematics nor pure methods but a combination of both.30 Teachers with more specialized content knowledge can better design lessons using math-science integration, use manipulatives in their lessons, and employ student-centered approaches to teaching mathematics.31

Experts suggest that educator preparation programs should structure requirements to address both subject matter knowledge (including common content knowledge and specialized content knowledge) and pedagogical content knowledge (including knowledge of content and students and knowledge of content and teaching).32 The approach described by Lee Shulman33—built off of early work begun by John Dewey and recently expanded by Deborah Ball—explains the complexity of teaching by delineating the domains of knowledge needed for teaching.

What should elementary teacher candidates learn about specialized mathematics content knowledge?

Elementary teachers need to grasp more than the mathematical knowledge and skills required in the curriculum. They need to master the mathematical knowledge that is unique to teaching.34 Examples of what teachers need to learn include being able to create and tailor representations of math problems to suit the "instructional purposes," being able to not only carry out but also explain algorithms for solving problems, and conducting error analysis.35 An effort to "unpack the mathematical work of teaching framework" to further explore what teachers should be able to do include activities such as, "Given conflicting explanations, determine which is valid and why," "Write a mathematically valid explanation for a process or concept," "Given a word problem, choose another word problem with the same structure," and "Given a set of representations, choose which does or does not show a particular idea."36

What should elementary teacher candidates learn about mathematics pedagogy?

Research on mathematics methods or pedagogy, although limited, also indicates the value of mathematics methods courses,37 including documented gains in mathematical knowledge for teaching.38 Research generally supports the importance of teachers' knowledge of fundamental math concepts as well as their ability to apply mathematics content in teaching (learned in mathematics methods courses), rather than their just knowing the mathematics content.39

Conclusion

In 2022, NCTQ revised its Elementary Mathematics Standard in keeping with the research that elementary teachers must be equipped with the mathematics content and pedagogical knowledge to effectively support learning by all students. NCTQ's examination of the opportunities a program provides to teacher candidates includes the domains of knowledge a teacher needs to bring to the classroom — the specialized mathematical content knowledge or knowledge of mathematics that is specific to teaching mathematics and pedagogical knowledge for teaching mathematics or the intersections between the mathematical content that comprises the curricula and knowledge of how student learn and effective methods to teach.40

Endnotes

  1. Werner, K., Acs, G., & Blagg, K. (2024). Comparing the long-term impacts of different child well-being improvements. Urban Institute. https://www.urban.org/sites/default/files/2024-03/Comparing_the_Long-Term_Impacts_of_Different_Child_Well-Being_Improvements.pdf

  2. Claessens, A., & Engel, M. (2013). How important is where you start? Early mathematics knowledge and later school success. Teachers College Record, 115(6), 1-29.

  3. Claessens, A., & Engel, M. (2013); Watts, T. W., Duncan, G. J., Siegler, R. S., & Davis-Kean, P. E. (2014). The groove of growth: How early gains in math ability influence adolescent achievement. Society for Research on Educational Effectiveness; Siegler, R. S., Duncan, G. J., Davis-Kean, P. E., Duckworth, K., Claessens, A., Engel, M., & Chen, M. (2012). Early predictors of high school mathematics achievement. Psychological Science, 23(7), 691-697; Duncan, G. J., & Magnuson, K. (2011). The nature and impact of early achievement skills, attention skills, and behavior problems. Whither Opportunity, 47-70.

  4. This figure represents 24% of fourth grade students in 2022. Data from "Table 203.10. Enrollment in public elementary and secondary schools, by level and grade: Selected years, fall 1980 through fall 2031," by the National Center for Education Statistics, 2023, Digest of Education Statistics. https://nces.ed.gov/programs/digest/d23/tables/dt23_203.10.asp

  5. National Assessment of Educational Progress. (2025). NAEP mathematics: National trends and student skills. U.S. Department of Education, National Center for Education Statistics. https://www.nationsreportcard.gov/reports/mathematics/2024/g4_8/national-trends/?grade=4

  6. Loewenberg Ball, D., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389-407.

  7. Horizon Research, Inc. (2019). Highlights from the 2018 NSSME+. http://horizon-research.com/NSSME/wp-content/uploads/2019/01/Highlights-from-2018-NSSME.pdf

  8. Sparks, Sarah D. (2020). The myth fueling math anxiety. Education Week. https://www.edweek.org/teaching-learning/the-myth-fueling-math-anxiety/2020/01

  9. Schaeffer, M. W., Rozek, C. S., Maloney, E. A., Berkowitz, T., Levine, S. C. and Beilock, S. L. (2021). Elementary school teachers' math anxiety and students' math learning: A large-scale replication. Developmental Science, 24(4), e13080. https://onlinelibrary.wiley.com/doi/abs/10.1111/desc.13080

  10. More information about the standard setting process can be found in the Technical Manual for Elementary Mathematics.

  11. Conference Board of the Mathematical Sciences. (2012). The mathematical education of teachers II. American Mathematical Society.

  12. NCTQ defines adequate math licensure tests as those that address at least half of all subtopics in a topic area (e.g., at least half of all subtopics in numbers and operations, across the aspects of procedural fluency, conceptual understanding, and application), and does not combine math with any other subjects in a test or subtest. For the full methodology and list of math licensure test ratings, see NCTQ's June 2025 State of the States mathematics report.

  13. Note the two programs that earn an A in the state. New York programs perform just as poorly under NCTQ's Reading Foundations standard, suggesting that state policy has broad repercussions for teacher candidates and their future students.

  14. The new regulations can be found on page 77 under "6A:9B-10.2 Elementary school (K-6)" in New Jersey's State Board of Examiners and Certification regulations.

  15. Blazar, D. (2015). Effective teaching in elementary mathematics: Identifying classroom practices that support student achievement. Economics of Education Review, 48, 16-29; Campbell, P. F., Nishio, M., Smith, T. M., Clark, L. M., Conant, D. L., Rust, A. H., DePiper, J. N., Frank, T. J., Griffin, M. J., & Choi, Y. (2014). The relationship between teachers' mathematical content and pedagogical knowledge, teachers' perceptions, and student achievement. Journal for Research in Mathematics Education, 45(4), 419-459; Hill, H., Charalambous, C. Y., & Chin, M. J. (2019). Teacher characteristics and student learning in mathematics: A comprehensive assessment. Educational Policy, 33(7), 1103-1134; Hill, H., Rowan, B., & Ball, D. (2005). Effects of teachers' mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42(2), 371-406; Kukla-Acevedo, S. (2009). Do teacher characteristics matter? New results on the effects of teacher preparation on student achievement. Economics of Education Review, 28, 49-57; Mapolelo, D. C., & Akinsola, M. K. (2015). Preparation of mathematics teachers: lessons from review of literature on teachers' knowledge, beliefs, and teacher education. International Journal of Educational Studies, 2(1), 01-12. Blazar (2015) found a relationship between teachers' mathematical content knowledge and two instructional characteristics: ambitiousness of instruction and frequency of errors and imprecision. While these characteristics also related to student achievement, the study did examine the direct relationship between teachers' math content knowledge and student achievement.

  16. Gorham Blanco, T., & Chamberlin, S. A. (2019). Pre-service teacher statistical misconceptions during teacher preparation program. The Mathematics Enthusiast, 16(1), 461-484.

  17. Banilower, E. R., Smith, P. S., Malzahn, K. A., Plumley, C. L., Gordon, E. M., & Hayes, M. L. (2018); Banilower, et al. (2013).

  18. Schmidt, W. H., & McKnight, C. (2002). Inequality for all: The challenge of unequal opportunity in American schools. New York: Teachers College Press, Columbia University.

  19. Hiebert, J., Berk, D., & Miller, E. (2017). Relationships between mathematics teacher preparation and graduates' analyses of classroom teaching. The Elementary School Journal, 117(4), 687-707; Hiebert, J., Berk, D., Miller, E., Gallivan, H., & Meikle, E. (2019). Relationships between opportunity to learn mathematics in teacher preparation and graduates' knowledge for teaching mathematics. Journal for Research in Mathematics Education, 50(1), 23-50; Morris, A. K., & Hiebert, J. (2017). Effects of teacher preparation courses: Do graduates use what they learned to plan mathematics lessons?. American Educational Research Journal, 54(3), 524-567; Suppa, S., DiNapoli, J., & Mixell, R. (2018). Teacher Preparation" Does" Matter: Relationships between Elementary Mathematics Content Courses and Graduates' Analyses of Teaching. Mathematics Teacher Education and Development, 20(2), 25-57.

  20. Boyd, D. J., Grossman, P. L., Lankford, H., Loeb, S., & Wyckoff, J. (2009). Teacher preparation and student achievement. Educational Evaluation and Policy Analysis, 31(4), 416-440. This study notes that its findings may differ from those in Harris & Sass (2011) because the Boyd study looked at "data on the characteristics of programs, courses, and field experiences," while the Harris study used course credit hours and hours of in-service training.

  21. Qian, H., & Youngs, P. (2016). The effect of teacher education programs on future elementary mathematics teachers' knowledge: a five-country analysis using TEDS-M data. Journal of Mathematics Teacher Education, 19(4), 371-396. This study found that (a) discrete structure and logic and (b) continuity and functions had the strongest effect on candidates' mathematics content knowledge.

  22. Harris, D. N., & Sass, T. R. (2011). Teacher training, teacher quality and student achievement. Journal of Public Economics, 95, 798-812. This study relates to several NCTQ standards. Although it meets the criteria for strong research, the study's findings run contrary to the conclusions of most strong research in the field.

  23. In this vein, a University of Virginia professor of psychology argued that elementary teachers need to be trained to understand and teach the "conceptual side of math," or else they cannot build a strong math foundation for their young students. Willingham, D. (2013). What the NY Times doesn't know about math instruction. Retrieved March 12, 2014 from http://www.danielwillingham.com/daniel-willingham-science-and-education-blog/what-the-ny-times-doesnt-know-about-math-instruction.

  24. Beckmann, S., Chazan, D., Cuoco, A., Fennell, F., & Findell, B. (2012). The Mathematical Education of Teachers II. In Issues in mathematics education/CBMS, Conference Board of the Mathematical Sciences (Vol. 17, pp. 1-86). Retrieved January 7, 2022 from https://cbmsweb.org/the-mathematical-education-of-teachers.

  25. National Council of Teachers of Mathematics. (2005, July).

  26. National Council of Teachers of Mathematics. (No Date). Executive Summary: Principles and standards for school mathematics. Retrieved April 26, 2021 from https://www.nctm.org/uploadedFiles/Standards_and_Positions/PSSM_ExecutiveSummary.pdf.

  27. Beckmann, S., Chazan, D., Cuoco, A., Fennell, F., & Findell, B. (2012).

  28. Masingila, J. O., Olanoff, D. E., & Kwaka, D. K. (2012). Who teaches mathematics content courses for prospective elementary teachers in the United States? Results of a national survey. Journal of Mathematics Teacher Education, 15(5), 347-358; Masingila, J. O., & Olanoff, D. (2021). Who teaches mathematics content courses for prospective elementary teachers in the USA? Results of a second national survey. Journal of Mathematics Teacher Education, 1-17.

  29. Max, B., & Welder, R. M. (2019). Engaging prospective elementary teachers in standards for mathematical practice within content courses for teachers. In Proceedings of the 41st Annual Conference of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 1141-1145).

  30. Greenberg, J., & Walsh, K. (2008). No Common Denominator. Washington, D.C.: National Council on Teacher Quality. However, a recent international comparative study claims that while both content knowledge and pedagogical content knowledge are important, "…CK may not necessarily need to develop before PCK…future reforms should consider the best ways to foster content and pedagogical content knowledge as distinct constructs rather than working under the assumption that developing CK is a necessary prerequisite for developing PCK." (p 16). Murray, E., Durkin, K., Chao, T., Star, J. R., & Vig, R. (2018). Exploring Connections between Content Knowledge, Pedagogical Content Knowledge, and the Opportunities to Learn Mathematics: Findings from the TEDS-M Dataset. Mathematics Teacher Education and Development, 20(1), 4-22.

  31. An, S. A. (2017). Preservice teachers' knowledge of interdisciplinary pedagogy: the case of elementary mathematics—science integrated lessons. ZDM, 49(2), 237-248; Greenstein, S., & Seventko, J. (2017). Mathematical Making in Teacher Preparation: What Knowledge Is Brought to Bear?. North American Chapter of the International Group for the Psychology of Mathematics Education; Son, J. W. (2016). Preservice teachers' response and feedback type to correct and incorrect student-invented strategies for subtracting whole numbers. The Journal of Mathematical Behavior, 42, 49-68.

  32. Loewenberg Ball, D., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special?. Journal of Teacher Education, 59(5), 389-407.

  33. Shulman, L. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1-23.

  34. Loewenberg Ball, D., Thames, M. H., & Phelps, G. (2008). p. 400.

  35. Ball, D. L., Hill, H. C., & Bass, H. (2005). Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide?. American Educator.

  36. Selling, S. K., Garcia, N., & Ball, D. L. (2016). What does it take to develop assessments of mathematical knowledge for teaching?: Unpacking the mathematical work of teaching. The Mathematics Enthusiast, 13(1), 35-51.

  37. Promoting Rigorous Outcomes in Mathematics and Science Education (2006, December). Knowing mathematics: What we can learn from teachers (Research Report, Vol. 2). East Lansing, MI: Michigan State University; Cavanna, J. M., Drake, C., & Pak, B. (2017). Exploring Elementary Mathematics Teachers' Opportunities to Learn to Teach. North American Chapter of the International Group for the Psychology of Mathematics Education; Santagata, R., Yeh, C., & Mercado, J. (2018). Preparing elementary school teachers to learn from teaching: A comparison of two approaches to mathematics methods instruction. Journal of the Learning Sciences, 27(3), 474-516; Giles, R. M., Byrd, K. O., & Bendolph, A. (2016). An investigation of elementary preservice teachers' self-efficacy for teaching mathematics. Cogent Education, 3(1), 1160523.

  38. Laursen, S. L., Hassi, M. L., & Hough, S. (2016). Implementation and outcomes of inquiry-based learning in mathematics content courses for pre-service teachers. International Journal of Mathematical Education in Science and Technology, 47(2), 256-275.

  39. Ball, D., Lubienski, S., & Mewborn, D. (2001). Research on teaching mathematics: The unsolved problem of teachers' mathematical knowledge. In V. Richardson (Ed.), Handbook on Research on Teaching (4th ed.). Washington, D.C.: American Educational Research Association; Guyton, E., & Farokhi, E. (1987). Relationships among academic performance, basic skills, subject matter knowledge, and teaching skills of teacher education graduates. Journal of Teacher Education, 38, N5.

  40. Loewenberg Ball, D., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389-407.

Show all endnotes Show less endnotes
Symbol

Get More Updates On Our Research